Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising

Abstract

图像去噪的判别模型学习由于其良好的去噪性能，近年来受到了人们的广泛关注。本文通过研究前馈去噪卷积神经网络(DnCNNs)的构建，将深度架构、学习算法和正则化方法在图像去噪方面的进展向前推进了一步。具体来说，利用残差学习和批处理归一化来加速训练过程，提高去噪性能。与通常在特定噪声水平上训练加性高斯白噪声（AWGN）的特定模型的现有判别去噪模型不同，我们的DnCNN模型能够处理具有未知噪声水平的高斯去噪（即，盲高斯去噪）。利用残差学习策略，DnCNN隐式去除隐藏层中隐藏的干净图像。这一特性促使我们训练单个DnCNN模型来处理多个常规图像去噪任务，如高斯去噪、单图像超分辨率和JPEG图像解块。我们的大量实验表明，我们的DnCNN模型不仅可以在几个常规的图像去噪任务中显示出较高的有效性，而且可以通过受益于GPU计算而有效地实现。

I. INTRODUCTION

图像去噪是低级视觉中经典但仍然活跃的主题，因为它是许多实际应用中不可或缺的一步。图像去噪的目标是从噪声观察y中恢复干净图像x，其遵循图像退化模型y = x + v。一个常见的假设是v是具有标准偏差σ的加性高斯白噪声（AWGN）。 从贝叶斯观点来看，当已知可能性时，图像先验建模将在图像去噪中起核心作用。在过去的几十年中，各种模型已经被用于建模图像先验，包括非局部自相似（NSS）模型[1]，[2]，[3]，[4]，稀疏模型[4]，[5] ，[6]，梯度模型[7]，[8]，[9]和马尔可夫随机场（MRF）模型[10]，[11]，[12]。特别是，NSS模型在最先进的方法中很受欢迎，如BM3D [2]， LSSC [4]， NCSR[6]和WNNM[13]。

尽管基于图像先验的去噪方法具有很高的去噪质量，但大多数方法都存在两个主要缺点。首先，这些方法在测试阶段通常涉及到一个复杂的优化问题，使得去噪过程耗时[6]，[13]。因此，大多数基于先验的方法很难在不牺牲计算效率的情况下获得高性能。其次，模型一般是非凸的，涉及多个人工选择的参数，为提高去噪性能提供了一定的余地。

为了克服基于先验的方法的局限性，最近开发了几种判别学习方法以在截断推理过程的背景下学习图像先验模型。得到的模型能够摆脱测试阶段的迭代优化过程。Schmidt和Roth[14]提出了一种级联收缩场(CSF)方法，将基于随机场的模型和展开的半二次优化算法结合在一个学习框架中。Chen等人[15]、[16]提出了一种可训练的非线性反应扩散(TNRD)模型，该模型通过展开固定数量的梯度下降推理步骤，先验学习专家改进的[12]图像域。其他一些相关的工作可以在[17][18]中找到。虽然CSF和TNRD在弥合计算效率和去噪质量之间的差距方面显示出了有希望的结果，但它们的性能本质上局限于先验的指定形式。具体来说，CSF和TNRD所采用的先验是基于分析模型的，在获取图像结构的全部特征方面受到了限制。此外，参数是通过逐阶段贪婪训练和各个阶段之间的关节微调来学习的，涉及到许多手工制作的参数。另一个不可忽略的缺点是它们训练了特定噪声水平的特定模型，在盲图像去噪中受到限制。

在本文中，我们将图像去噪作为一个普通的判别学习问题，而不是使用显式图像先验来学习判别模型，利用前馈卷积神经网络(CNN)将噪声从噪声图像中分离出来。使用CNN的原因有三方面。首先，[19]架构非常深的CNN有效地提高了挖掘图像特征的能力和灵活性。第二，CNN训练的正则化和学习方法取得了长足的进步，包括整流线性单元(ReLU)[20]、批量归一化[21]和残差学习[22]。这些方法可用于CNN中，加快训练过程，提高去噪性能。第三，CNN非常适合在现代强大的GPU上进行并行计算，可以用来提高运行时性能。

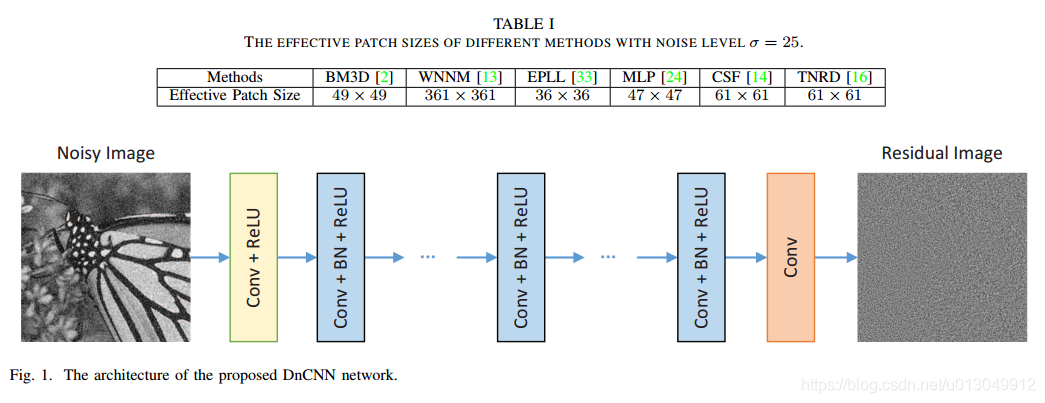
我们将提出的去噪卷积神经网络称为DnCNN。 不是直接输出去噪图像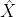，而是将所提出的DnCNN设计成预测残留图像，即噪声观察和潜在清洁图像之间的差异。也就是说，所提出的DnCNN通过隐层中的操作隐式地删除了隐藏的干净图像。进一步引入批量归一化技术，稳定和提高DnCNN的训练性能。结果表明，残差学习和批处理归一化是相互促进的，两者的集成可以有效地加快训练速度，提高去噪性能。

虽然本文旨在设计一种更有效的高斯降噪器，但我们观察到当v是地面实况高分辨率图像与低分辨率图像的双三次上采样之间的差异时，高斯降噪的图像劣化模型可以转换为单个 图像超分辨率（SISR）问题;类似地，JPEG图像去块问题可以通过将v作为原始图像和压缩图像之间的差异来通过相同的图像劣化模型来建模。 从这个意义上讲，SISR和JPEG图像去块可以被视为一般图像去噪问题的两种特殊情况，尽管在SISR和JPEG去块中，噪声与AWGN有很大不同。很自然地会问是否有可能训练CNN模型来处理这种一般的图像去噪问题？ 通过分析DnCNN与TNRD之间的联系[16]，我们提出扩展DnCNN来处理几种一般的图像去噪任务，包括高斯去噪，SISR和JPEG图像去块。

大量实验表明，我们用一定噪声水平训练的DnCNN可以产生比BM3D [2]，WNNM [13]和TNRD [16]等最先进方法更好的高斯去噪效果。 对于具有未知噪声水平的高斯去噪（即盲高斯去噪），具有单个模型的DnCNN仍然优于BM3D [2]和TNRD [16]针对特定噪声水平进行训练。当扩展到几个一般图像去噪任务时，DnCNN也可以获得有希望的结果。 此外，我们展示了仅针对三种一般图像去噪任务训练单个DnCNN模型的有效性，即，盲高斯去噪，具有多个放大因子的SISR，以及具有不同质量因子的JPEG解块。

这项工作的贡献总结如下：

1）提出了一种端到端可训练的深度CNN高斯去噪算法。与现有的基于深度神经网络的直接估计潜清洁图像的方法相比，该网络采用残差学习策略从噪声观测中去除潜清洁图像。

2）我们发现残差学习和批处理归一化对CNN的学习有很大的帮助，不仅可以加快训练速度，而且可以提高去噪性能。对于具有一定噪声水平的高斯去噪，DnCNN在定量指标和视觉质量上都优于最先进的方法。

3）我们的DnCNN可以很容易地扩展到处理一般的图像去噪任务。我们可以训练单一的DnCNN模型进行高斯盲去噪，并且比针对特定噪声水平训练的其他方法获得更好的性能。此外，有希望解决三个一般的图像去噪任务，即盲高斯去噪，SISR和JPEG去块，只有一个DnCNN模型。

本文的其余部分组织如下。第二节简要介绍了有关工作。第三节首先给出了所提出的DnCNN模型，然后将其扩展到一般的图像去噪。在第四节中，我们进行了广泛的实验来评估DnCNNs。最后，第五节提出了一些结束语。

II. RELATED WORK

A. Deep Neural Networks for Image Denoising
针对深度神经网络去噪问题，已有多种尝试。在[23]中，Jain和Seung提出利用卷积神经网络(tional neural network, CNNs)进行图像去噪，并声称CNNs具有与MRF模型相似甚至更好的表示能力。在[24]中，多层感知器(MLP)成功应用于图像去噪。[25]采用叠加稀疏去噪自编码器方法对高斯噪声进行去除，与K-SVD[5]效果相当。在[16]中，提出了一种可训练的非线性反应扩散(TNRD)模型，该模型通过展开一定数量的梯度下降推理步骤，可表示为前馈深度网络。在上述基于深度神经网络的方法中，MLP和TNRD均能达到较好的性能，能够与BM3D相竞争。然而，对于MLP[24]和TNRD[16]，针对一定的噪声水平，训练一个特定的模型。据我们所知，CNN对于一般图像去噪的研究还没有展开。

B. Residual Learning and Batch Normalization
近年来，卷积神经网络由于能够方便地获取大规模数据集和深度学习方法的进步，在处理各种视觉任务方面取得了巨大的成功。训练CNN模型的代表性成果有:校正线性单元[20]、深度与宽度折衷[19]、[26]、参数初始化[27]、基于梯度的优化算法[28]、[29]、[30]、批处理归一化[21]、残差学习[22]。其他因素，如在现代强大的gpu上高效的训练实施，也有助于CNN的成功。对于高斯去噪，从一组高质量的图像中容易产生足够的训练数据。本文主要研究CNN图像去噪的设计与学习。接下来，我们将简要回顾与DnCNN相关的两种方法，即，残差学习和批处理归一化。

1) Residual Learning:
CNN的残差学习[22]最初是为了解决性能下降的问题，即，随着网络深度的增加，训练精度也开始下降。通过假设残差映射比原始的未引用映射更容易学习，残差网络明确地学习了几个叠加层的残差映射。利用这种残差学习策略，可以很容易地训练出深度极高的CNN，提高了图像分类和目标检测[22]的准确率。

提出的DnCNN模型也采用残差学习公式。 与使用许多残差单元（即，同一性快捷方式）的残差网络[22]不同，我们的DnCNN使用单个残余单元来预测残留图像。通过分析残差学习公式与TNRD[16]的关系，进一步解释了残差学习公式的原理，并将其扩展到解决几种常用的图像去噪任务。需要注意的是，在残差网络[22]出现之前，在单图像超分辨率[31]和彩色图像去马赛克[32]等低阶视觉问题中，已经采用了残差图像预测策略。然而，据我们所知，目前还没有直接对残差图像进行去噪预测的工作。

2）Batch Normalization:

小批量随机梯度下降（SGD）已广泛用于训练CNN模型。 尽管小批量SGD具有简单性和有效性，通过内部协变位移，其训练效率大大降低[21]，即训练期间内部非线性输入分布的变化。为了减轻内部协变位移的影响，提出了批量归一化[21]的方法，即在每一层非线性之前，结合归一化步骤和尺度和位移步骤。对于批处理规范化，每次激活只添加两个参数，并且可以通过反向传播更新它们。批处理规范化具有训练快、性能好、初始化灵敏度低等优点。有关批处理规范化的详细信息，请参阅[21]。

到目前为止，基于cnn的图像去噪的批处理归一化研究尚未开展。我们通过实证发现，将残差学习和批处理归一化相结合，可以得到快速稳定的训练和较好的去噪效果。

III. THE PROPOSED DENOISING CNN MODEL

在本节中，我们提出了所提出的去噪CNN模型，即DnCNN，并扩展它以处理几个一般的图像去噪任务。 通常，针对特定任务训练深度CNN模型通常涉及两个步骤：（i）网络架构设计和（ii）从训练数据学习模型。对于网络架构设计，我们修改VGG网络[19]以使其适用于图像去噪，并根据最先进的去噪方法中使用的有效色块大小设置网络的深度。对于模型学习，我们采用残差学习公式，并将其与批量归一化相结合，实现快速训练，提高去噪性能。最后，我们讨论了DnCNN与TNRD[16]之间的联系，并将DnCNN扩展到几个一般的图像去噪任务中。

A.Network Depth

根据[19]中的原则，我们将卷积过滤器的大小设置为3×3，但是删除所有池化层。因此，深度为d的DnCNN感受野应为(2d+1)x (2d+1)。增加感受野大小可以利用较大图像区域中的上下文信息。 为了在性能和效率之间进行更好的权衡，架构设计中的一个重要问题是为DnCNN设置适当的深度。

已经指出，去噪神经网络的感受野大小与去噪方法的有效patch大小相关[23]，[24]。 此外，高噪声水平通常需要更大的有效patch大小来捕获更多的上下文信息以进行恢复[34]。因此，通过固定噪声水平σ= 25，我们分析了几种主要去噪方法的有效patch尺寸，以指导我们的DnCNN的深度设计。在BM3D [2]中，非局部相似贴片在大小为25×25的局部窗口中自适应搜索两次，因此最终有效贴片大小为49×49。与BM3D类似，WNNM[13]使用了更大的搜索窗口，并迭代执行非局部搜索，从而产生了相当大的有效patch大小(361×361)。MLP[24]首先使用大小为39×39的patch生成预测的patch，然后使用大小为9×9的filter对输出的patch进行平均，其有效patch大小为47×47。具有五个阶段的CSF [14]和TNRD [16]涉及总共十个卷积层，其滤波器尺寸为7×7，并且它们的有效patch尺寸为61×61。

表I总结了在噪声水平σ= 25的不同方法中采用的有效patch尺寸。可以看出，EPLL [33]中使用的有效patch尺寸最小，即36×36。
有趣的是，验证感受野大小类似于EPLL的DnCNN能否与主流去噪方法竞争。因此，对于具有一定噪声水平的高斯去噪，我们将DnCNN的感受野大小设置为35×35，对应深度为17。对于其他一般的图像去噪任务，我们采用较大的感受野，深度设置为20。

B.Network Architecture

我们的DnCNN的输入是噪声观察y = x + v。诸如MLP [24]和CSF [14]之类的判别去噪模型旨在学习映射函数F（y）= x来预测潜在的清洁图像。对于DnCNN，我们采用残差学习公式来训练残差映射，然后我们得到。 形式上，所需残差图像与噪声输入的估计残差图像之间的平均均方误差

(1)

可以采用损失函数来学习DnCNN中的可训练参数Θ。这里表示N个噪声干净的训练图像（patch）对。 图1示出了用于学习R（y）的所提出的DnCNN的架构。 在下文中，我们将解释DnCNN的体系结构和减少边界伪影的策略。

1）Deep Architecture:

给定深度为D的DnCNN，有三种类型的层，如图1所示，具有三种不同的颜色。 （i）Conv + ReLU：对于第一层，使用64个大小为3x3xc的滤波器来生成64个特征图，然后将整流线性单元用于非线性。这里c表示图像通道的数量，即灰度图像的c = 1，彩色图像的c = 3。 （ii）Conv + BN + ReLU：对于层，使用64个大小为3x3x64的过滤器，并在卷积和ReLU之间添加批量标准化[21]。 （iii）Conv：对于最后一层，使用大小为3x3x64的c个滤波器来重建输出。

综上所述，我们的DnCNN模型有两个主要特点:采用残差学习公式来学习R(y)，并结合批量归一化来加速训练，提高去噪性能。通过与ReLU的卷积，DnCNN可以通过隐藏层逐步将图像结构从噪声观测中分离出来。这种机制类似于在EPLL和WNNM等方法中采用的迭代噪声去除策略，但是我们的DnCNN是采用端到端的方式进行训练的。稍后我们将对残差学习和批处理规范化相结合的原理进行更多的讨论。

2）Reducing Boundary Artifacts:

在许多低级别的视觉应用程序中，通常要求输出图像的大小与输入图像的大小保持一致。这可能会导致边界伪影。在MLP[24]中，预处理阶段对噪声输入图像的边界进行对称填充，而在CSF[14]和TNRD[16]中，每个阶段之前都进行相同的填充策略。与上述方法不同，我们在卷积之前直接填充零，以确保中间层的每个特征图具有与输入图像相同的大小。我们发现简单的零填充策略不会导致任何边界伪影。 这个好的属性可能归因于DnCNN的强大能力。

C. Integration of Residual Learning and Batch Normalization for Image Denoising

图1所示的网络既可以训练原映射F(y)预测x，也可以训练残差映射R(y)预测v。根据[22]，当原映射更像恒等映射时，残差映射更容易优化。值得注意的是，噪声观测y更像潜在的干净图像x，而不是残留图像v(尤其是在噪声水平较低的情况下)。因此，F(y)比R(y)更接近恒等映射，残差学习公式更适合图像去噪。

图2显示了在基于梯度的优化算法和网络体系结构的相同设置下使用这两种学习公式获得的平均PSNR值，有/无批次归一化。 注意，采用两种基于梯度的优化算法：一种是具有动量的随机梯度下降算法（即SGD），另一种是Adam算法[30]。首先，我们可以观察到残差学习公式比原映射学习收敛更快、更稳定。同时，如果没有批处理归一化，传统SGD的简单残差学习无法与TNRD (28.92dB)等最先进的去噪方法竞争。我们认为这种不足的表现是由于训练过程中网络参数的变化所引起的内部协变漂移[21]造成的。因此，我们采用批处理规范化来解决这个问题。其次，我们观察到，通过批量归一化，学习残差映射(红线)比学习原始映射(蓝线)收敛更快，去噪性能更好。其中，SGD和Adam优化算法都能使具有残差学习和批处理归一化的网络获得最好的结果。也就是说，去噪效果最好的不是SGD或Adam算法，而是残差学习公式和批处理归一化的集成。

实际上，我们可以注意到，在高斯去噪中，残差图像和批处理归一化都与高斯分布有关。在高斯去噪中，残差学习和批处理归一化很有可能相互受益。下面的分析可以进一步验证这一点。

• 一方面，残差学习得益于批处理规范化。这很简单，因为批处理规范化为CNNs提供了一些优点，比如减轻了内部协变移位问题。从图2中可以看出，虽然没有批处理归一化的残差学习(绿线)收敛速度较快，但仍不如批处理归一化的残差学习(红线)。
• 另一方面，批处理规范化得益于残差学习。如图2所示，在没有残差学习的情况下，批处理归一化甚至会对收敛产生一定的不利影响(蓝线)。通过残差学习，可以利用批处理归一化来加速训练，提高性能(红线)。注意，每个小批量是一小组（例如，128个）图像。 在没有残差学习的情况下，输入强度和卷积特征与它们的相邻特征相关联，并且层输入的分布也依赖于每个训练小批量中的图像的内容。通过残差学习，DnCNN通过隐层中的操作隐式地去除隐藏的干净图像。这使得每一层的输入都是高斯分布的，相关性较低，与图像内容的相关性也较低。因此，残差学习还可以帮助批处理标准化，以减少内部协变位移。

综上所述，将残差学习和批处理归一化相结合，不仅可以加快和稳定训练过程，而且可以提高去噪性能。

D. Connection with TNRD

我们的DnCNN也可以解释为一阶段TNRD的推广[15]，[16]。 通常，TNRD旨在通过大量降级 – 清洁训练图像对训练针对以下问题的判别解决方案。

(2)

这里N表示图像大小，λ表示正则化参数，fk*x表示图像x与第k个滤波器核fk的卷积，ρk（·）表示在TNRD模型中可调整的第k个惩罚函数。 对于高斯去噪，我们设置。

第一阶段的扩散迭代可以被解释为在起始点y处执行一个梯度下降推断步骤，其由下式给出

(3)

其中是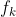的伴随滤波器（即，是通过将滤波器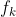旋转180度获得的），α对应于步长，并且。对于高斯去噪，我们得到和等式（3）等同于以下表达式

(4)

其中v1是x关于y的估计残差。

由于影响函数φk（·）可以被认为是应用于卷积特征映射的逐点非线性，因此，方程（4）实际上是一个双层前馈CNN。 从图1中可以看出，所提出的CNN架构从三个方面进一步概括了一阶段TNRD：（i）用ReLU取代影响函数以简化CNN训练；（ii）增加CNN深度，提高图像特征建模能力;（iii）与批处理规范化相结合，提高性能。与单阶段TNRD的联系为解释残差学习在基于cnn的图像恢复中的应用提供了见解。方程（4）中的大多数参数来自方程（2）的先前项的分析。 在这个意义上，DnCNN中的大多数参数代表图像先验。

有趣的是，即使噪声不是高斯分布的(或者高斯的噪声级别未知)，我们仍然可以利用方程(3)得到v1

(5)

注意，方程(5)适用于多种噪声分布，如广义高斯分布。很自然地，对于SISR和JPEG压缩造成的噪声，也可以这样假设。训练单个CNN模型可以完成多个常规图像去噪任务，如噪声水平未知的高斯去噪、多个上标度因子的SISR去噪、不同质量因子的JPEG去噪。

方程（4）也可以解释为从劣化的观察y中去除潜在清洁图像x以估计残留图像v的操作。对于这些任务，即使噪声分布也很复杂，可以预期我们的DnCNN还可以通过逐渐去除隐藏层中的潜在干净图像来稳健地预测残留图像。

E.Extension to General Image Denoising

现有的判别高斯去噪方法，如MLP、CSF和TNRD，都训练了固定噪声级[16]、[24]的特定模型。在未知噪声的高斯去噪中，一种常用的方法是先估计噪声水平，然后使用相应噪声水平训练的模型。这使得去噪结果受到噪声估计精度的影响。此外，这些方法不能应用于非高斯噪声分布的情况，如SISR和JPEG去块。

我们在第III-D节中的分析显示了DnCNN在一般图像去噪中的潜力。 为了证明这一点，我们首先将我们的DnCNN扩展为具有未知噪声水平的高斯去噪。 在训练阶段，我们使用来自各种噪声水平（例如，）的噪声图像来训练单个DnCNN模型。对于噪声级属于噪声级范围的测试图像，利用学习的单DnCNN模型可以在不估计噪声级的情况下进行降噪。

我们通过学习单个模型来进一步扩展我们的DnCNN，用于几个一般的图像去噪任务。 我们考虑三个特定任务，即盲高斯去噪，SISR和JPEG去块。在训练阶段，我们利用大范围噪声级的AWGN图像，多个上标度因子的下采样图像，以及不同质量因子的JPEG图像来训练单个DnCNN模型。实验结果表明，学习的单DnCNN模型在三种常规图像去噪任务中均能取得较好的去噪效果。

IV. EXPERIMENTAL RESULTS

A. Experimental setting

1) Training and Testing Data:对于已知或未知噪声水平的高斯去噪，我们跟随[16]使用400幅大小为180×180的图像进行训练。我们发现使用更大的训练数据集只能带来微不足道的改进。为了训练DnCNN进行具有已知噪声水平的高斯去噪，我们考虑三个噪声水平，即σ= 15,25和50。我们将patch大小设置为40×40，裁剪128×1; 600个patch来训练模型。 我们将具有已知特定噪声水平的高斯去噪的DnCNN模型称为DnCNN-S。

为了训练单个DnCNN模型进行盲高斯去噪，我们将噪声水平的范围设置为，patch尺寸为50×50。128×3000个patch裁剪以训练模型。我们将用于盲高斯去噪任务的单个DnCNN模型称为DnCNN-B。

对于测试图像，我们使用两种不同的测试数据集进行全面的评估，一种是包含来自Berkeley dataset (BSD68)[12]的68幅自然图像的测试数据集，另一种是包含12幅图像的测试数据集，如图3所示。需要注意的是，这些图像都被广泛应用于高斯去噪方法的评估中，而在训练数据集中并不包含这些图像。

除了灰度图像去噪之外，我们还训练盲目彩色图像去噪模型，称为CDnCNNB。 我们使用BSD68数据集的彩色版本进行测试，并采用Berkeley分割数据集中剩余的432个彩色图像作为训练图像。 噪声水平也设置在[0,55]和裁剪了128×3000个大小为50×50的patch来训练模型。

为了学习三种常用图像去噪任务的单个模型，如[35]，我们使用了一个数据集，该数据集由来自[36]的91幅图像和来自Berkeley分割数据集的200幅训练图像组成。在[0,55]范围内加入一定噪声水平的高斯噪声，生成噪声图像。SISR输入是通过第一个双三次下采样生成的，然后使用缩减因子2,3和4对高分辨率图像进行双三次上采样。JPEG解块输入是通过使用MATLAB JPEG编码器压缩质量因子从5到99的图像生成的。所有这些图像都被视为单个DnCNN模型的输入。 总的来说，我们生成128×8,000个图像patch（大小为50×50）对进行训练。 在小批量学习期间使用patch对上的基于旋转/翻转的操作。参数用DnCNN-B初始化。 我们将这三个一般图像去噪任务的单个DnCNN模型称为DnCNN-3。 为了测试DnCNN-3，我们对每个任务采用不同的测试集，详细描述将在第IV-E节中给出。

2) Parameter Setting and Network Training:为了捕获足够的空间信息进行去噪，我们将DnCNN-S的网络深度设置为17，将DnCNN-B和DnCNN-3的网络深度设置为20。采用公式（1）中的损失函数来学习用于预测残差v的残差映射R（y）。我们通过[27]中的方法初始化权重，并使用SGD，权重衰减为0.0001，动量为0.9，小批量大小为128。我们为DnCNN模型训练了50个时期。在50个时期，学习率从1e-1到1e-4呈指数衰减。

我们使用MatConvNet软件包[37]来训练提出的DnCNN模型。除非另有说明，否则所有实验均在Matlab（R2015b）环境中进行，该环境在具有Intel（R）Core（TM）i7-5820K CPU 3.30GHz和Nvidia Titan X GPU的PC上运行。在GPU上分别训练DnCNN-S，DnCNNB / CDnCNN-B和DnCNN-3需要大约6小时，一天和三天。

B. Compared Methods

我们将提出的DnCNN方法与几种最先进的去噪方法进行比较，包括两种非局部相似性方法（即BM3D [2]和WNNM [13]），一种生成方法（即EPLL [33]）），三种基于判别训练的方法（即MLP [24]，CSF [14]和TNRD [16]）。注意，CSF和TNRD通过GPU实现是高效的，同时提供良好的图像质量。实现代码从作者的网站下载，我们的实验使用默认参数设置。我们DnCNN模型的测试代码可以在https://github.com/cszn/DnCNN下载。

C. Quantitative and Qualitative Evaluation

BSD68数据集上不同方法的平均PSNR结果如表II所示。可以看出，DnCNN-S和DnCNN-B都可以获得比竞争方法更好的PSNR结果。与基准的BM3D相比，MLP和TNRD方法的PSNR增益显著，约为0.35dB。根据[34]，[38]，很少有方法能超过BM3D平均0.3dB以上。相比之下，我们的DnCNN-S模型在三个噪声级别上都比BM3D要好0.6dB。特别是，即使是没有已知噪声水平的单一模型，我们的DnCNN-B仍然可以胜过针对已知特定噪声水平进行训练的竞争方法。值得注意的是，当σ= 50时，DnCNN-S和DnCNN-B的性能均优于BM3D约0.6dB，这与[38]中BM3D（0.7dB）的估计PSNR非常接近。

表III列出了图3中12幅测试图像不同方法的PSNR结果。对于每个噪声级别的图像，最佳PSNR结果用粗体突出显示。可以看出，在大多数图像中，DnCNN-S的PSNR最高。具体而言，DnCNN-S在大多数图像上的表现优于竞争方法0.2dB至0.6dB，并且仅在两个图像House和Barbara上实现最佳结果，这两个图像由重复结构支配。这一结果与[39]的研究结果一致:非局部均值法通常对结构规律性和重复性的图像效果较好，而基于判别训练的方法通常对纹理不规则的图像效果较好。实际上，这在直观上是合理的，因为具有规则和重复结构的图像与非局部相似先验很好地满足;反之，纹理不规则的图像会削弱这种特定先验的优势，导致较差的结果。

图4-5展示了不同方法的可视化结果。可以看出，BM3D、WNNM、EPLL和MLP容易产生过于光滑的边缘和纹理。在保留锐利边缘和细节的同时，TNRD可能会在平滑区域生成伪影。相比之下，DnCNN-S和DnCNN-B不仅可以恢复锐利的边缘和精细的细节，而且在平滑区域也能产生视觉上令人愉悦的效果。

对于彩色图像去噪，CDnCNN-B和基准CBM3D之间的视觉比较如图6-7所示。

可以看出，CBM3D在某些区域产生假色伪影，而CDnCNN-B可以恢复具有更自然色彩的图像。此外，CDnCNN-B可以生成比CBM3D具有更多细节和更锐利边缘的图像。

图8显示了相对于DnCNN-B / CDnCNN-B模型的不同噪声水平，BM3D / CBM3D的平均PSNR改善。可以看出，我们的DnCNN-B / CDnCNN-B型号在很宽的噪声水平范围内始终优于BM3D / CBM3D。该实验结果证明了训练单个DnCNN-B模型在广泛的噪声水平范围内处理盲高斯去噪的可行性。

D.Run Time

除了视觉质量，图像恢复方法的另一个重要方面是测试速度。表四给出了256×256、512×512、1024×1024三种图像去噪方法的运行时间，噪声等级为25。由于CSF、TNRD和我们的DnCNN方法非常适合在GPU上进行并行计算，我们也给出了相应的GPU上的运行时间。我们使用Nvidia cuDNNv5深度学习库来加速所提出的DnCNN的GPU计算。在[16]中，我们不计算CPU和GPU之间的内存传输时间。可以看出，所提出的DnCNN在CPU上具有较高的速度，比MLP和CSF两种判别模型都要快。虽然速度慢于BM3D和TNRD，但是考虑到图像质量的提高，我们的DnCNN在CPU实现上还是很有竞争力的。对于GPU时间，所提出的DnCNN实现了非常吸引人的计算效率，例如，它可以在60ms内对具有未知噪声水平的512×512大小的图像进行去噪，这是相对于TNRD的明显优势。

E. Experiments on Learning a Single Model for Three General Image Denoising Tasks

为了进一步展示所提出的DnCNN模型的能力，我们对单个DnCNN-3模型进行了训练，用于三种常用的图像去噪任务，包括盲高斯去噪、SISR和JPEG图像去块。据我们所知，现有的方法中没有一种仅用一个模型来处理这三个任务。因此，对于每个任务，我们将DnCNN-3与特定的最先进的方法进行比较。下面我们将描述每个任务的比较方法和测试数据集：

• 对于高斯去噪，我们使用最先进的BM3D和TNRD进行比较。BSD68数据集用于测试性能。对于BM3D和TNRD，我们假设噪声水平已知。
• 对于SISR，我们考虑两种最先进的方法，即TNRD和VDSR [35]。 TNRD训练了每个上升因子的特定模型，而VDSR [35]训练了所有三个升级因子（即2,3和4）的单个模型。 我们采用[35]中使用的四个测试数据集（即Set5和Set14，BSD100和Urban100 [40]）。
• 对于JPEG图像去块，我们将DnCNN-3与两种最先进的方法进行比较，即AR-CNN [41]和TNRD [16]。 AR-CNN方法分别训练了JPEG质量因子10,20,30和40的四种特定模型。 对于TNRD，训练了三个用于JPEG质量因子10,20和30的模型。 与[41]中一样，我们采用Classic5和LIVE1作为测试数据集。

表V列出了不同方法对不同常规图像去噪任务的平均PSNR和SSIM结果。可以看出，即使我们训练一个DnCNN-3模型来完成这三种不同的任务，它在高斯去噪方面仍然优于非盲的TNRD和BM3D。对于SISR来说，它大大超过了TNRD，与VDSR不相上下。对于JPEG图像去锁，DnCNN-3在PSNR方面比AR-CNN高出约0.3dB，在所有质量因子上都比TNRD高出约0.1dB PSNR增益。

图9和图10为不同SISR方法的可视化比较。可以看出，DnCNN-3和VDSR都能产生锐利的边缘和精细的细节，而TNRD则容易产生模糊的边缘和扭曲的线条。图11为不同方法的JPEG去块结果。可以看出，我们的DnCNN-3可以恢复直线，而AR-CNN和TNRD容易产生扭曲的直线。图12给出了一个额外的例子来显示该模型的容量。我们可以看到，DnCNN- 3可以产生视觉上令人愉悦的输出结果，即使输入的图像被不同区域的不同级别的几种失真所破坏。

V.CONCLUSION

本文提出了一种用于图像去噪的深度卷积神经网络，利用残差学习将噪声从噪声观测中分离出来。将批量归一化和残差学习相结合，加快训练过程，提高去噪性能。与传统的针对特定噪声水平训练特定模型的判别模型不同，我们的单一DnCNN模型能够处理未知噪声水平的盲高斯去噪。此外，我们展示了训练单个DnCNN模型处理三种一般图像去噪任务的可行性，包括具有未知噪声水平的高斯去噪，具有多个放大因子的单图像超分辨率，以及具有不同质量因子的JPEG图像去块。大量实验结果表明，该方法不仅能定量、定性地获得良好的图像去噪性能，而且通过GPU实现具有良好的运行时间。

 

转载自Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising_Adagrad的博客-CSDN博客

版权归属原作者，如有问题，欢迎留言联系删除

 

 

赞赏

微信赞赏 支付宝赞赏